Gaming Selection Bias in Gaming through Doubly Robust Estimation

By Eunki Min

The bane of every researcher’s existence, selection bias makes no exception for the gaming industry. In fact, selection bias is a common problem in our experiments at Happy Elements, since we often study a naturalistic sample–our users–and we can’t always enforce strict randomization in our tests. Selection bias arises when the treated and control groups differ systematically. When selection bias exists, A/B tests or naive regressions will be misleading. For example, if active users are more likely to experience new features in the pilot stage, then the OLS regression may overestimate the improvement in user experiences (since these users are familiar with the game and are delighted by the rush of new features).

Fortunately, even when the treatment is assigned disproportionately, we can still control the systematic differences in assignment with our large-scale data. In fact, if we can perfectly explain the treatment rule with observables, the treatment is almost as good as random.

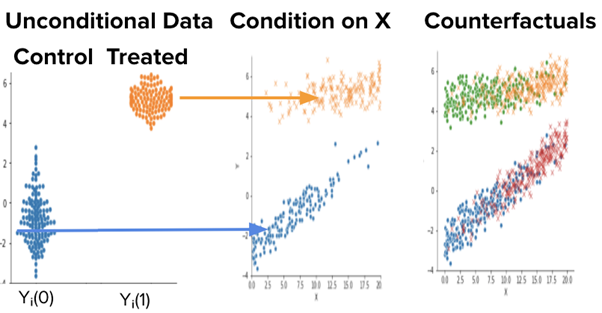
Formally, we assume Strong Ignorability, which requires the counterfactual outcomes when treated (Y1) and not treated (Y0) are independent of the treatment (D) given observable data (X). In the above example, we may use measures of the user’s activeness (X) to explain the treatment assignment (D) rule.

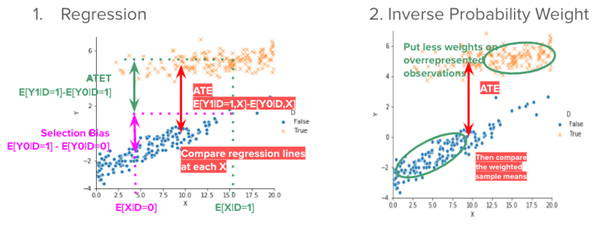
With the Strong Ignorability assumption, we may estimate the true causal parameter with regression or Inverse Probability Weighting (IPW). The regression method estimates the effect of X on Y for each treated and control group, then computes the average differences between these two lines. Regression requires the correct specification of the estimation equation. The IPW uses X to predict the probability of being treated (i.e., propensity score, p(X) = P[D=1|X]), then puts more weights on observations that are underrepresented. IPW requires propensity scores to be correctly specified. Moreover, the control and treatment groups should overlap so that p(X) does not become 0 or 1.

Validating the regression and IPW analyses’ assumptions can be difficult, so we try to circumvent the problem using the Doubly Robust (DR) estimation. There are no formal tests on whether the regression model or the propensity scores are correctly specified, so we need to use our best judgment to decide if each of these assumptions hold. With the DR estimator, we can still consistently estimate the causal effect even if one of the regression or IPW analyses is incorrect. DR augments the IPW analysis with an adjustment term from the regression model. Theoretically and empirically, DR is proven to have desirable properties when at least one of the two assumptions is correct.

The downside of DR is that when both regression or propensity models are incorrect, this method may underperform to a greater extent than each model alone. To guarantee the quality of our analysis, we always cross-check the Doubly Robust estimators with regression and propensity models’ results.